Resolución Final - Final C (Febrero 2025 ✨) - Física 03 CBC Cátedra Única

Volver a Final

FÍSICA 03 CBC

CÁTEDRA ÚNICA

Final C (Febrero 2025 ✨)

Ejercicio 1:

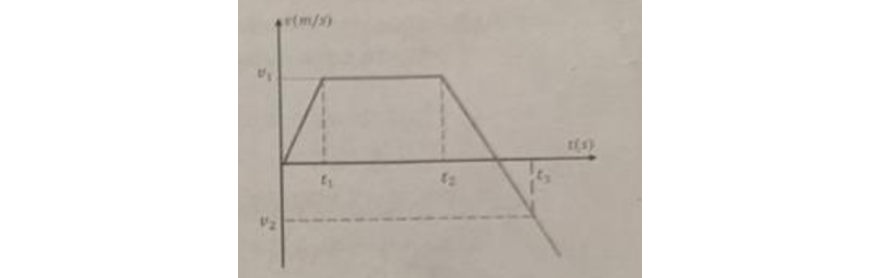
A partir del gráfico dado, que corresponde a la velocidad en función del tiempo para un móvil que se mueve de manera rectilínea en varias etapas...

Datos: $v_1 = 6 \text{ m/s}$, $v_2 = -6 \text{ m/s}$, $t_1 = 3 \text{ s}$, $t_2 = 10 \text{ s}$ y $t_3 = 12 \text{ s}$

a) El desplazamiento del móvil entre $t = 0 \text{ s}$ y $t = t_3$ vale:

$\square$ $-21 \text{ m}$ $\square$ $42 \text{ m}$ $\square$ $13.5 \text{ m}$ $\square$ $102 \text{ m}$ $\square$ $51 \text{ m}$ $\square$ $0 \text{ m}$

b) La aceleración media entre $t = t_1$ y $t = t_3$ vale:

$\square$ $-0.66 \text{ m/s}^2$ $\square$ $0.66 \text{ m/s}^2$ $\square$ $-2.66 \text{ m/s}^2$ $\square$ $2.66 \text{ m/s}^2$ $\square$ $-1.33 \text{ m/s}^2$ $\square$ $1.33 \text{ m/s}^2$

Ejercicio 2:

Un objeto es disparado horizontalmente desde una altura de $30 \text{ m}$. Se observa que al llegar al piso golpea con un ángulo (respecto de la horizontal) de $\alpha = 30°$. Puede despreciarse el rozamiento con el aire.

a) ¿Cuánto se desplazó en dirección horizontal?

$\square$ $240 \text{ m}$ $\square$ $207.8 \text{ m}$ $\square$ $103.9 \text{ m}$ $\square$ $51.9 \text{ m}$ $\square$ $69.4 \text{ m}$ $\square$ $80 \text{ m}$

b) Entre la altura inicial y el momento de golpear el piso puede afirmarse que:

$\square$ Su energía mecánica aumenta

$\square$ Su energía mecánica disminuye

$\square$ Su energía cinética disminuye

$\square$ Su energía potencial gravitatoria aumenta

$\square$ El trabajo del peso es positivo

$\square$ El trabajo de las fuerzas no conservativas es negativo

Ejercicio 3:

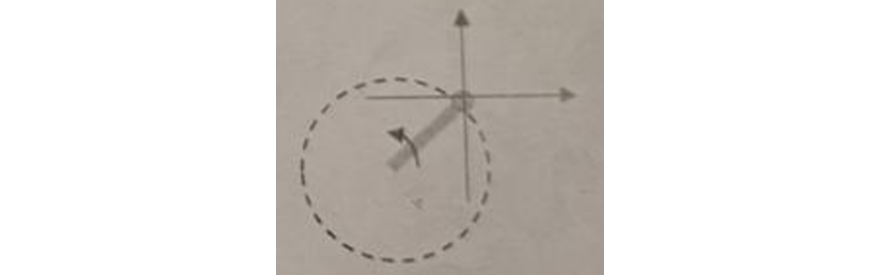
Una bolita de $500 \text{ g}$ se encuentra en un plano horizontal unida a una barra (sin masa) de $8 \text{ cm}$ de largo. Inicialmente la bolita se encuentra en reposo y se pone en movimiento circular (acelerando uniformemente en la dirección de la flecha) hasta que, después de $5$ vueltas, alcanza una frecuencia de $90 \text{ rpm}$.

a) ¿Cuánto vale su aceleración angular?

$\square$ $0.25 \text{ 1/s}^2$ $\square$ $0.71 \text{ 1/s}^2$ $\square$ $3.14 \text{ 1/s}^2$ $\square$ $1.41 \text{ 1/s}^2$ $\square$ $6.28 \text{ 1/s}^2$ $\square$ $2.82 \text{ 1/s}^2$

b) Dibuje la fuerza resultante sobre la bolita en el sistema que se muestra en el dibujo.

Ejercicio 4:

Un cable sostiene una caja cúbica de $20 \text{ cm}$ de arista que está parcialmente sumergida en un líquido de densidad $2.3 \, \frac{kg}{dm^3}$. La tensión del cable es de $30 \text{ N}$ y la caja está sumergida $7 \text{ cm}$.

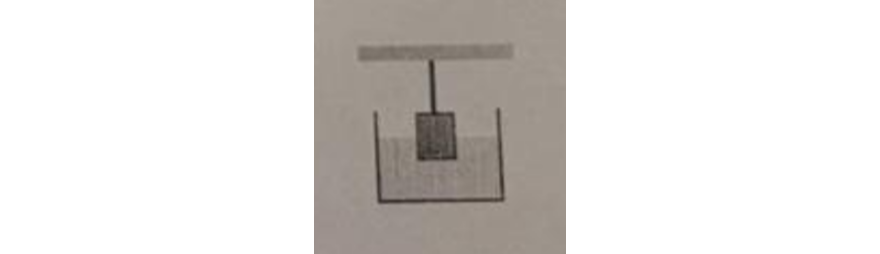
a) ¿Cuánto vale la presión del líquido sobre la cara inferior del cubo?

$\square$ $320 \text{ Pa}$ $\square$ $161 \text{ Pa}$ $\square$ $1610 \text{ Pa}$ $\square$ $2300 \text{ Pa}$ $\square$ $1127 \text{ Pa}$ $\square$ $230 \text{ Pa}$

b) Si se aumenta la densidad del cubo sin variar sus dimensiones...

$\square$ Aumenta el empuje

$\square$ El empuje disminuye

$\square$ La presión sobre la cara inferior aumenta

$\square$ La presión sobre la cara inferior disminuye

$\square$ Aumenta la tensión de la cuerda

$\square$ La tensión de la cuerda no varía

Ejercicio 5:

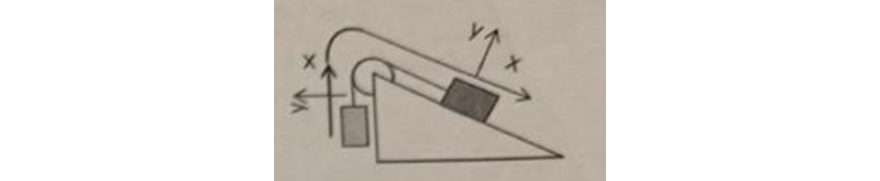
El sistema de la figura está formado por un cuerpo $m_2 = 35 \text{ kg}$ que se encuentra vinculado por una soga ideal a otro de masa $m_1 = 15 \text{ kg}$. El cuerpo se mueve en un plano inclinado a 30° con rozamiento. El coeficiente de rozamiento dinámico vale $0.5$, en tanto que el coeficiente estático es de $0.8$.

En un determinado momento se observa que la caja que cuelga está descendiendo a $2 \text{ m/s}$. En esas condiciones:

a) ¿Cuánto vale, aproximadamente, la tensión de la cuerda en ese momento?

$\square$ $350 \text{ N}$ $\square$ $265 \text{ N}$ $\square$ $202 \text{ N}$ $\square$ $175 \text{ N}$ $\square$ $150 \text{ N}$ $\square$ $56 \text{ N}$

b) Cuando el sistema se detiene, el módulo de la fuerza de rozamiento vale

$\square$ $\mu_e(m_2 - m_1 \, g) \cos(30°)$

$\square$ $m_1 \, g$

$\square$ $m_1 \, g \, \sin(30°)$

$\square$ $\mu_e(m_1 \, g \, \cos(30°))$

$\square$ $(m_2 \, \sin(30°) - m_1) \, g$

$\square$ $(m_1 - m_2 \, \sin(30°)) \, g$

Ejercicio 6:

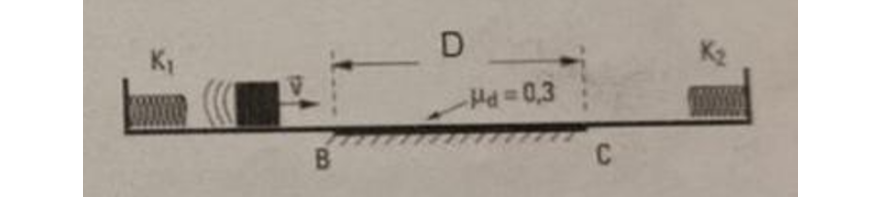
Un cuerpo de $4 \text{ kg}$ se desplaza a una velocidad de $15 \text{ m/s}$ después de ser impulsado desde el reposo por el resorte de constante $k_1$.

Datos: $D = 2.5 \text{ m}$, $k_1 = 5000 \text{ N/m}$, $k_2 = 8000 \text{ N/m}$

a) La compresión máxima del resorte $k_1$ que impulsó a cuerpo:

$\square$ $0.42 \text{ m}$ $\square$ $0.3 \text{ m}$ $\square$ $0.6 \text{ m}$ $\square$ $0.5 \text{ m}$ $\square$ $0.2 \text{ m}$ $\square$ $0.84 \text{ m}$

b) El trabajo de las fuerzas no conservativas desde que arranca hasta que la partícula se detiene:

$\square$ $-300 \text{ J}$ $\square$ $-450 \text{ J}$ $\square$ $-150 \text{ J}$ $\square$ $300 \text{ J}$ $\square$ $450 \text{ J}$ $\square$ $-45 \text{ J}$

CURSO RELACIONADO

Física 03

2025 ÚNICA

¿Te ayudan nuestros exámenes?
Sumate a nuestro curso, donde te enseño toda la materia de forma súper simple. 🥰

Ir al curso

¿Listx para rendir?

Elegí la modalidad y empezá 👉

Interactivo Simulacro